Lý giải định luật bảo toàn năng lượng chỉ với một đồng xu, vị phó giáo sư này giải thích dễ đến mức trẻ con cũng hiểu được

Năng lượng là câu trả lời của rất nhiều vấn đề hiện nay, từ chiếc điều khiển điều hòa hết pin cho tới những khu vực công nghiệp khổng lồ cung cấp việc làm cũng như sản phẩm cho hàng triệu người. Vậy năng lượng là thứ kì diệu gì?

Đó là câu hỏi khó, vậy nên ta sẽ trả lời nó dựa vào ba anh chàng A, B và C dưới đây. Tôi hoàn toàn có thể đặt là X, Y và Z nhưng tôi không thích thế, và một phần nhỏ là do nguyên bản của bài viết này trên tạp chí Wired của phó giáo sư vật lý Rhett Allain tại Đại học Đông Nam Louisiana đặt tên họ là Alby, Bobby và Cami.

Và đây là câu chuyện của 3 chàng trai ấy:

Alby có 10 USD và cho đi hết hai người còn lại. Bobby có 5 USD và Cami thì có được 4,99 USD.

Có một xu thiếu, không biết ai lấy mất nhỉ? Nó đi đâu rồi? Khi mà Alby hào phóng cho tiền các bạn, có lẽ đồng xu ấy đã rơi đâu mất rồi.

Nhưng kể cả khi Alby đánh rơi nó, đồng xu đó vẫn tồn tại. Tổng tiền cộng vào vẫn đủ 10 USD.

Đây cũng có thể gọi là luật bảo toàn tiền bạc được. Dù chuyện gì xảy ra (mua đồ, làm rơi, hay “biếu” tên trấn lột cùng lớp), thì tổng tiền vẫn không đổi trước và sau sự kiện biến động mất tiền diễn ra. Còn một điều nữa bạn nên biết về tiền, đó là chúng không có thực. Chúng chỉ là công cụ cho phép con người trao đổi thuận tiện hơn và chỉ là chuẩn mực ta đặt ra để so sánh hàng hóa mà thôi. Nhưng mà không có tiền không được ...

Vậy thì tiền thì liên quan gì đến năng lượng và định luật bảo toàn năng lượng? Thực ra thì năng lượng cũng giống tiền. Hãy sử dụng ví dụ dưới, khi mà ấn một quả bóng vào trong một cái ống có sẵn một cái lò xo bên trong, đây sẽ là 3 trạng thái diễn ra:

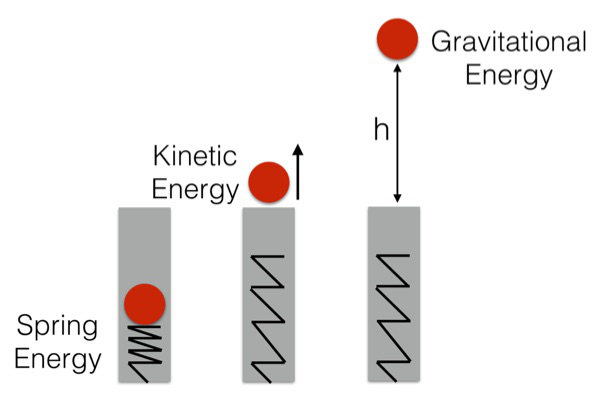
Lò xo bắn quả bóng lên – Cái lò xo ấy tích trữ năng lượng để làm được hành động này, quả bóng do tác động của năng lượng phát ra bởi cái lò xo đã bắn lên không. Bây giờ đến quả bóng có năng lượng, được gọi là động năng. Khi quả bóng lên tới độ cao cao nhất mà nó có thể với tới, vận tốc của nó trở về 0 và tại điểm đó, quả bóng lại bị lực hấp dẫn kéo xuống.

Bây giờ, nếu như bạn tính năng lượng có thể có trước khi lò xo bắn quả bóng ra, có thể số đo ấy bằng 10 Joule (J). Khi phóng ra, có thể nó chỉ còn có 9J động năng và 1J thuộc năng lượng của lực hấp dẫn do quả bóng lúc này đang ở trên cao. Khi mà quả bóng đang leo đến độ cao cao nhất, nó có ít động lượng hơn năng lượng từ lực hấp dẫn. Khi nó đã leo đến mức cao nhất, nó có đủ 10J năng lượng tiềm tàng của lực hấp dẫn.

Loại lực thay đổi liên tục, nhưng tổng số đo của lực lại là một hằng số. Lực cũng như tiền, chúng đều được bảo toàn.

Bây giờ hãy lấy một ví dụ khác, nhỏ bé hơn. Hạt nhân của một nguyên tử thường là một sự kết hợp của các proton và các neutron. Nguyên tố carbon 14 có tất cả 6 proton và 8 neutron, nhưng nó không hoàn toàn ổn định. Theo thời gian, nguyên tử carbon 14 sẽ bị phân rã phóng xạ, qua một quá trình mang tên phân rã beta. Việc phân rã này để lại một nguyên tử nitro được gọi là nitro 14 và một electron duy nhất. Chúng đều có động lượng, bởi lẽ khối là một loại năng lượng nữa, một thứ năng lượng thuộc công thứ E = mc² nổi tiếng.

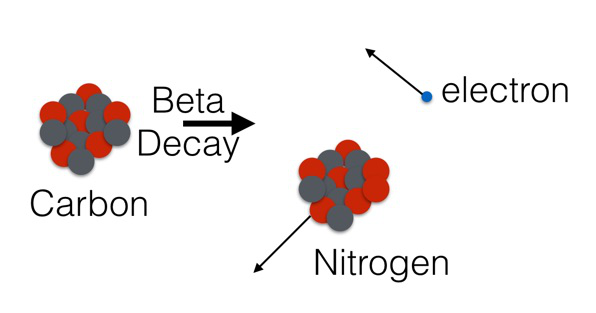
Đây là phần thú vị này. Dựa trên sự khác biệt của khối carbon và khối nitro, ta có thể dựa vào việc phân rã để tìm ra tổng lượng năng lượng. Ta cứ cho nó bằng 10J cho dễ tính. Ta cũng có thể đo đạc tốc độ và tính toán được động năng từ các electron kia. Ví dụ như ta có được giá trị 3,99J từ carbon, thì ta có thể có được 6J từ nitro, vậy là có 0,1J năng lượng không biết đi đâu mất. Vậy có nghĩ là năng lượng không được bảo tồn?

Không phải, có nghĩa là chỗ năng lượng đó đang ở đâu đó nhưng không hề mất đi.

Điều này đã xảy ra trong một thí nghiệm hồi năm 1930, khi mà Wolfgang Pauli – nhà vật lý học người Mỹ gốc Áo-Thụy Điển gợi lên rằng có một hạt khác trong quá trình phân rã beta giữ chỗ năng lượng (đáng giá 0,1J) này. Ông đã đúng, hạt đó mang tên neutrino.

Quả là kì diệu, khi mà con người chỉ nghĩ ra phép tính này bởi vì nó ... tiện lợi cho mình, bởi tổng năng lượng trước và sau khi biến cố xảy ra phải bằng nhau, Nếu như chúng không bằng nhau, ắt hẳn là có một yếu tố bí ẩn gì đó mà ta chưa biết. Ta không hề nghĩ tới việc năng lượng bị mất đi, mà đã cứng đầu khẳng định rằng một thế lực vô hình nào đang cầm giữ chỗ năng lượng thiếu ấy. Thế mà ta đã đúng.